- Date : 2022-09-05
- Last modified date : 2022-09-12
Route Optimization using Quantum Annealing in AWS Braket

- Route Optimization using Quantum Annealing in AWS Braket
- [Traveling Salesman Problem TSP](#traveling-salesman-problem-tsp)
- [Methods](#methods)
- [TSP as graph problem](#tsp-as-graph-problem)
- [Binary Encoding](#binary-encoding)
- [Libraries](#libraries)
- [Generation of Synthetic Data](#generation-of-synthetic-data)
- [Clustering](#clustering)
- [Distance Matrix](#distance-matrix)
- [Set up Graph](#set-up-graph)
- [QUBO for TSP](#qubo-for-tsp)
- [Classical Simulated Annealing](#classical-simulated-annealing)
- [Quantum Annealing on D-Wave with HPO for Lagrange Parameter](#quantum-annealing-on-d-wave-with-hpo-for-lagrange-parameter)
- [Meta-Optimized Route](#meta-optimized-route)
- [Visualization of Meta-Optimized Route using Folium](#visualization-of-meta-optimized-route-using-folium)
- [Summary](#summary)
- [References](#references)
이번 포스팅에서는 AWS Braket에서 사용할 수 있는 D-Wave Quantum Annealing을 활용하여 최소비용경로를 계산하고, 이를 시각화하는 프로젝트를 소개하려고 한다.
양자컴퓨팅은 최근 물리학계와 계산과학계에서 주목받고 있는 양자머신 기반의 새로운 컴퓨팅 기술이다. 이 기술은 아직 발전의 초기단계이지만, Google이나 IBM 등의 회사에서 일부 서비스를 제공하면서 이미 경쟁이 벌어지고 있다. 오늘은 이러한 양자컴퓨팅에 포함되는 최적화 기술인 양자어닐링(Quantum Annealing)에 대한 기초지식 및 간단한 예제 프로젝트를 소개한다. 대부분의 내용은 D-Wave 홈페이지의 기술적 설명과 D-Wave Braket 인스턴스 안에 있는 예제코드를 참고하였음을 밝힌다.
Introduction to D-Wave Quantum Annealing
I’m not happy with all the analyses that go with just the classical theory, because Nature isn’t classical, dammit, and if you want to make a simulation of nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem, because it doesn’t look so easy. It’s not a Turing machine, but a machine of a different kind. — Richard Feynman, 1981
오늘날 극도로 발전된 슈퍼컴퓨터의 강력한 연산능력에도 불구하고, 여전히 많은 복잡한 문제는 기존 시스템으로 해결될 수 없다. 양자컴퓨팅은 이런 어려운 문제를 해결하기 위해, 완전히 새로운 접근방식을 추구하는 차세대 컴퓨팅 분야라고 할 수 있다. 그리고 물리학과의 미래 밥줄이기도 하다.
Feynman이 칼텍에서 유명한 강의를 했던 1981년 이후, 양자컴퓨팅 분야에서는 많은 발전이 이루어졌다. 오늘날 양자컴퓨터의 2가지 주요 아키텍처는 Gate-model(Circuit-model) 및 Quantum Annealing이다.
- Gate-model Quantum Computing은 고전컴퓨터에서 부울(Boolean) 게이트를 사용하는 것과 유사하게, 양자게이트(Quantum Gate) 기반으로 계산 알고리즘을 구현한다.
- 양자 어닐링(Quantum Annealing)은 낮은 에너지 상태에서 시스템을 초기화하고, 해결하려는 문제의 매개변수를 점진적으로 도입한다. 시스템의 느린 변화는 최적해에 해당하는 낮은 에너지 상태로 종료될 가능성을 만든다.
오늘 소개할 양자어닐링은 D-Wave 양자컴퓨터에서 사용가능한 Advantage TM 및 2000Q device와 같은 단일양자 알고리즘으로 구현되며, 양자처리장치(Quantum Processing Unit, QPU)를 기반으로 작동한다. 현재 D-Wave에서는 자사의 양자어닐링 기술이 게이트 모델 양자컴퓨팅의 최첨단 성능을 능가한다고 주장하고 있다.
D-Wave's Quantum Computer Systems
D-Wave 회사의 양자시스템은 머신의 양자역학적 작동을 위해 절대영도에 가까운 온도로 유지되고, 주변환경과 반드시 격리되어야 하는 QPU가 포함되어 있다. 이 시스템은 다음과 같은 요구사항을 만족한다.
- Closed-loop Cryogenic Dilution Refrigerator System을 사용하여 극저온 환경을 만들고, QPU는 15mK 미만의 온도에서 작동한다.
- Radio Frequency(RF)-shielded Enclosure와 Magnetic Shielding subsystem을 사용하여 전자파 차폐환경을 만든다.
다음 그림은 D-Wave에서 소개하는 양자컴퓨터를 보여준다.

이러한 양자컴퓨터는 D-Wave QPU로 작동한다. QPU는 qubit 또는 coupler라는 작은 금속루프의 격자(lattice)이다. 9.2K 이하의 온도에서 이 루프는 초전도체(Superconductor)가 되어 양자역학적 효과를 발휘한다고 알려져있다.
D-Wave 최신 시스템은 Advantage-TM QPU는 5,000개 이상의 qubit와 35,000개의 coupler가 있다. 이를 위해 D-Wave에서는 백만개 이상의 Josephson Junction을 사용하였고, 현존하는 가장 복잡한 초전도 집적회로를 만들었다고 한다.

2 WorkFlow : Formulation and Sampling
복잡한 설명은 대충 건너뛰고, 양자컴퓨터를 사용하여 문제를 어떻게 해결할 수 있을까? 문제를 해결하는 2가지 단계는 다음과 같다.
- Formulate your problem as an objective function
목적 함수는 최적화되어야 하는 문제의 수학적 표현이다. 양자컴퓨팅의 경우, 이는 문제에 대한 최적해를 위해 가장 낮은 에너지를 갖는 2차 모델(Quadratic Model)을 의미한다. - Find good solutions by sampling
Sampler는 목적함수의 낮은 에너지 상태에서 샘플링하는 프로세스를 의미한다. Quadratic Model을 D-Wave의 Quantum, Classical, Hybrid Quantum-Classical 샘플러 중 하나에 제출하여 좋은 해를 찾을 수 있다.
Sampler는 D-Wave Leap 이라는 환경에서 원격으로 실행되거나, CPU에서 로컬로 실행될 수 있는데, 이는 solver로 알려진 컴퓨팅 리소스 위에서 실행된다. 또한, 일부 고전적인 샘플러는 실제로 샘플링이 아닌 Brute-force 방식으로 작은 문제를 풀이하는데, 이를 solver라고도 한다.
Objective Functions
대부분의 최적화 문제에서 그런 것처럼, Quantum Annealing에서도 문제의 수학적 표현인 목적함수(Objective Function)이 필요하다. Solver가 하나의 QPU인 경우, '에너지'는 QPU의 qubit를 나타내는 이진변수(Binary Variable)로 구성된 함수이다. 즉, 목적함수를 구성하는 변수는 0 또는 1의 값을 갖는다. Quantum-Classical Hybrid Solver를 사용할 경우, 목적함수의 모양은 더 추상적일 수 있다.
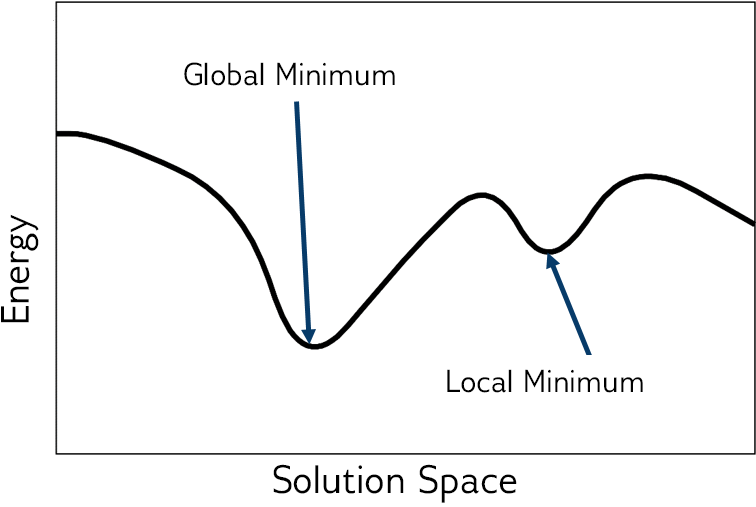
위 그림에서 보이는 것처럼 목적함수의 에너지가 낮을수록 그에 대응하는 해는 더 최적에 가까워진다. 최적해는 일반적으로 해 공간(Solution Space)의 전역적 최소점(Global Minimum)에 해당한다.
Simple Objective Example
예를 들면, $x + 1 = 2$와 같은 간단한 방정식을 풀이하는 것을 고려하자. 대수적인 방식으로 풀이한다면 당연히 답은 $x = 1$이다.
그러나 최적화 관점에서 샘플링을 통해 풀이한다고 하면, 다음과 같이 재수식화해야 한다.
$$ \begin{aligned}\text{E}(x) &= [2-(x+1)]^2\&= (1-x)^2\end{aligned} $$
이 경우 수식 $\min_x { (1 - x)^2 }$이 의미하는 것은 $(1 - x)^2$이라는 함수가 그려지는 공간에서 전역적 최소점을 찾고 이에 대응하는 $x$ 값을 찾으라는 것이다. 제곱은 음수값을 제거하는 효과이다.
Quadratic Models
D-Wave Quantum Annealing에서 문제를 풀이하기 위한 목적함수 설계는 다음과 같은 3종류의 Quadratic Model로 분류된다.
- Binary Quadratic Models (BQM) : Unconstrained / Binary Variables
BQM은 True or False 결정에 대한 최적화를 위해 사용된다. 예를 들면, '안테나가 신호를 전송해야 하는가?' '네트워크 노드에서 오류가 발생했는가?' 등의 질문에 답할 수 있다. - Constrained Quadratic Models (CQM) : Constrained / Integer or Binary Variables
CQM은 실수나 정수 이진변수와 하나 이상의 제약조건을 갖는 문제의 최적화에 사용된다. - Discrete Quadratic Models (DQM) : Unconstrained / Discrete Variables
DQM은 여러 개별적인 옵션의 최적화 문제에 사용된다. 예를 들면, '직원 A는 어느 교대조에 근무해야 하는가?', '지도의 상태는 여러 색상 중 어떤 색으로 표시되어야 하는가?' 등의 질문에 답할 수 있다.
이러한 Quadratic Model은 공통적으로 하나의 항에 1개 또는 2개의 변수를 갖는다. 간단한 예시를 보자.
$$ D = Ax + By + Cxy $$
여기서 $A$, $B$, $C$는 상수이다. 단일변수 $x$, $y$와 연관되어 $Ax$, $By$ 항이 존재하여 편향을 나타낸다. 2개의 변수가 결합된 항 $Cxy$를 2차 항이라고 한다. 우리의 Quantum Annealing이 풀고자 하는 최적화 문제의 목적함수는 항상 위와 같은 형태로 표현될 수 있어야 한다.
그럼 제약조건은 어떻게 표현될까? 아래에서 다시 설명하겠지만, 일반적으로 페널티 항을 목적함수에 추가하는 방식으로 이루어진다.
What is Quantum Annealing?
이제부터 양자어닐링의 원리를 조금 더 자세히 설명할 것인데, 이를 위해 기초적인 물리지식을 복습해보자.
Applicable Problems
양자어닐링 과정은 최종적으로 목적함수의 낮은 에너지에 대응되는 최적해를 반환한다. 크게 2종류의 문제가 있다.
최적화(Optimization) 문제 : 최적화 문제에서는 가능한 많은 조합 중에서 가장 최적희 해를 찾고자 한다. 예를 들면, '어떤 물건을 이 트럭에 실어야 하는가? 아니면 다음 트럭에 실어야 하는가?'와 같은 일정문제(Scheduling Challenges)와 '여행 중인 영업사원이 다른 도시를 방문하기 위해 선택해야 하는 가장 효율적인 경로는 무엇인가?'와 같은 문제가 포함된다. 이 글에서 후자의 질문을 TSP라는 이름으로 풀이하는 예제를 소개할 것이다.
물리학은 이런 종류의 문제들을 에너지 최소화(Energy Minimization) 문제로 구성할 수 있으므로, 최적화 문제 해결에 도움이 될 수 있다. 물리학의 기본규칙은 모든 것이 최소 에너지 상태를 추구하는 경향이 있다는 것이다. 물체는 언덕 아래로 미끄러진다. 뜨거운 것은 시간이 지나면 식는다. 이러한 원리는 양자역학의 세계에서도 마찬가지이다. 양자어닐링은 양자역학적 원리로 작동하는 머신을 사용하여 문제의 저에너지 상태를 찾음으로써, 최적 또는 거의 최적에 가까운 요소의 조합을 찾아낸다.
샘플링(Sampling) 문제 : 낮은 에너지 상태에서 많은 샘플링을 시도하여 에너지 함수의 형태를 유추하는 것은 현실의 확률적 모델을 학습하려는 기계학습 문제에 특히 유용하다. 샘플은 주어진 매개변수 집합에 대한 모델의 상태정보를 제공하고, 이는 모델을 개선하는데 활용될 수 있다.
머신러닝에서 말하는 확률모델은 기존에 알고 있던 지식의 격차와 데이터의 오류를 설명하여 불확실성을 명시적으로 처리한다. 여기서 확률분포는 노이즈를 포함하여 모델에서 관측되지 않은 양과 데이터의 관계를 나타낸다. 데이터 분포는 유한한 샘플 집합을 기반으로 근사화된다. 모델은 관찰된 데이터로부터 추론하여 사전분포(Prior Distribution)을 사후분포(Posterior Distribution)으로 변환하고, 이 과정에서 학습이 발생한다. 훈련이 충분히 이루어지면, 학습된 분포는 데이터를 생성한 분포와 비슷해지므로 관찰되지 않은 데이터에 대한 예측이 가능해진다. 이렇게 에너지 기반 분포에서 샘플링하는 것은 D-Wave 양자컴퓨터의 문제해결 방식과 매우 잘 어울리는 계산집약적인 작업이다.
How Quantum Annealing Works in D-Wave QPUs
큐비트(Qubit)로 불리는 양자비트(Quantum Bit)는 QPU를 구성하는 초전도루프의 가장 낮은 에너지 상태를 의미한다. 이러한 상태는 순환전류와 자기장으로 구성된다. 기존 비트와 마찬가지로 큐비트는 0 또는 1의 상태를 가질 수 있지만, 양자객체이기 때문에 0 상태와 1 상태의 양자역학적 중첩(Superposition) 상태에 있을 수 있다. 양자어닐링 과정이 종료되면, 각 큐비트는 중첩상태에서 0 또는 1의 고전적인 상태로 붕괴(Collapse)된다. 다음 그림은 큐비트의 상태가 자기장의 방향에 의해 제어되는 상황을 보여준다.
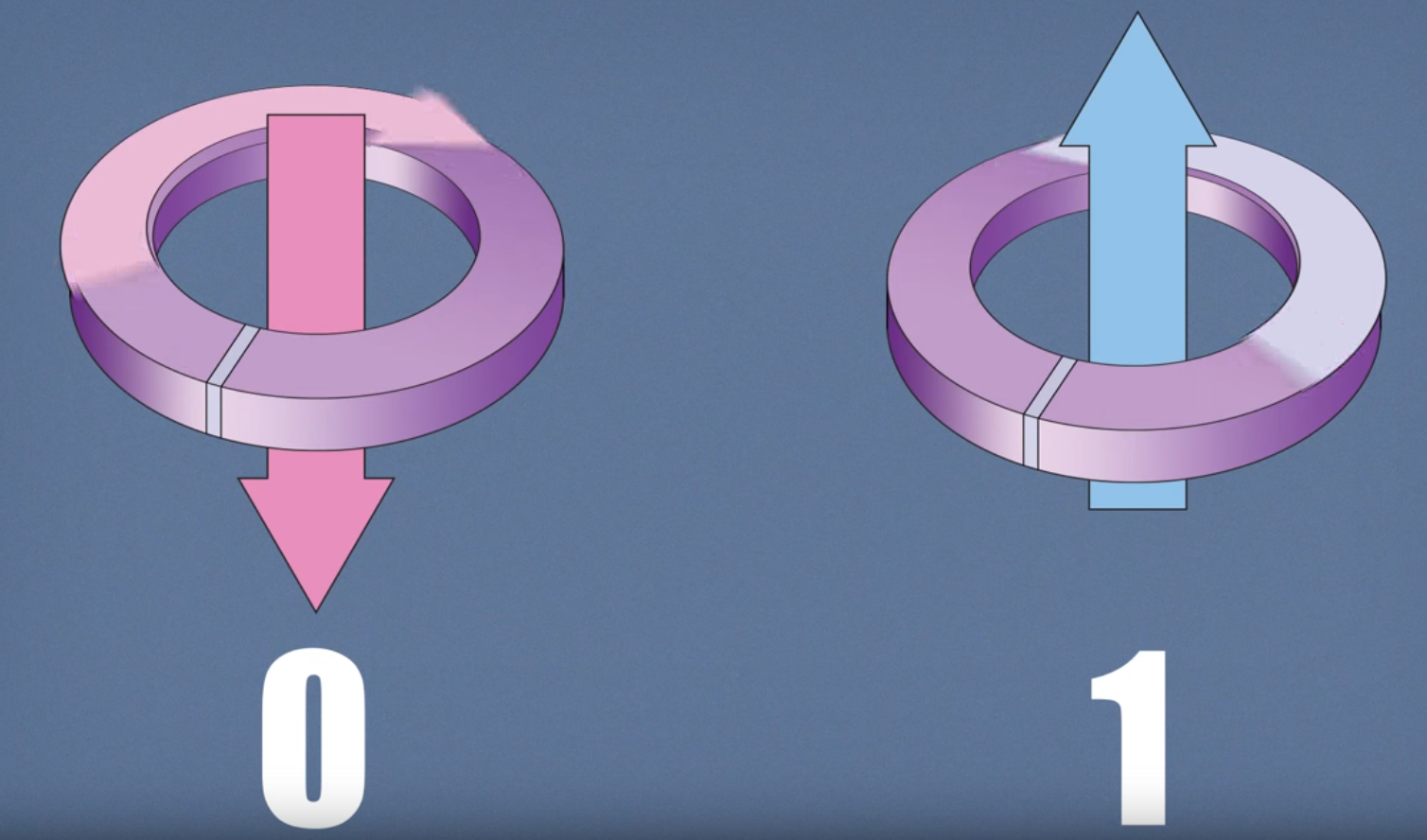
이러한 과정은 에너지 다이어그램으로 표현될 수 있다. 아래의 그림을 보자.
다이어그램은 (a), (b), (c)에 표시된 것처럼 시간이 지남에 따라 변화한다. 양자어닐링이 시작되려면 최소값이 하나인 상태 (a)가 하나만 있어야 한다. 양자어닐링이 시작되고 퍼텐셜 장벽이 높아지며 에너지 다이어그램은 양자역학에서의 이중우물전위(Double-well Potential) (b) 모양으로 바뀐다. 여기서 왼쪽 저점은 0 상태에 해당하고, 오른쪽 저점은 1 상태에 해당한다. 큐비트는 어닐링이 끝날 때 두 저점 중 하나에 위치하게 된다.
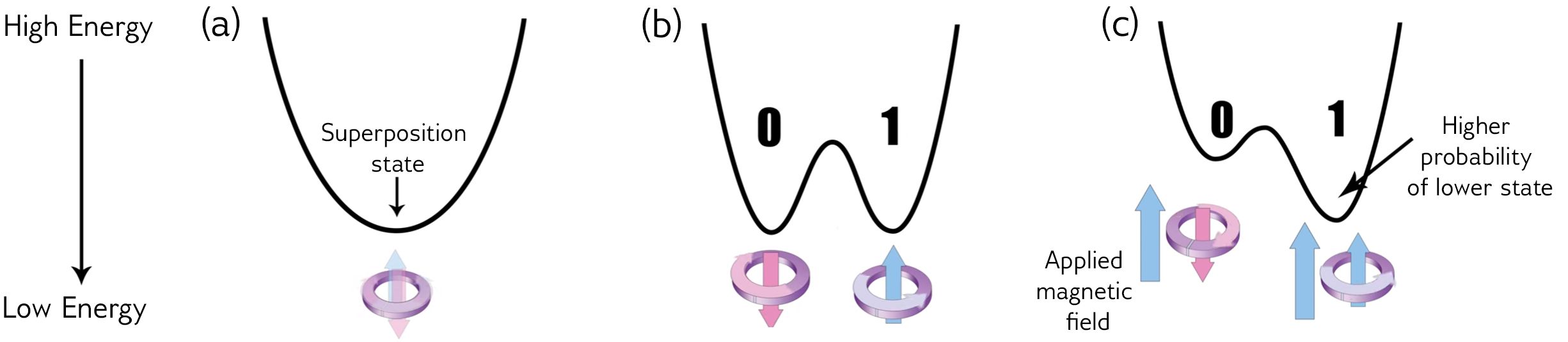
다른 모든 조건이 동일하다면, 큐비트가 0 또는 1 상태로 종료될 확률은 동등하게 50%이다. 그러나 큐비트 (c)에 외부자기장(External Magnetic Field)를 적용하여 0 또는 1 상태로 붕괴할 확률을 제어할 수 있다. 이 자기장은 이중우물전위 퍼텐셜을 기울여서, 큐비트가 더 낮은 점에서 끝날 확률을 높인다. 외부자기장을 제어하는 프로그래밍 가능한 양을 바이어스(Bias)라고 하며, 큐비트는 Bias가 있는 상태에서 에너지를 최소화한다.
그러나 이것만으로는 충분하지 않다. 큐비트의 진정한 힘은 서로 연결되어 영향을 미칠 때 나타난다. 이는 커플러(Coupler)라는 장치로 수행된다. 커플러는 두 큐비트가 같은 상태 또는 반대 상태로 끝나도록 만들 수 있다. 큐비트의 bias와 마찬가지로, 결합된 큐비트 사이의 상관가중치(Correlation Weight)는 결합강도(Coupling Strength)를 설정하여 프로그래밍될 수 있다.
결국 프로그래밍 가능한 bias와 weight가 양자컴퓨터에서 문제를 정의하는 수단이 된다.
커플러를 사용할 때 얽힘(Entanglement)라는 또 다른 양자현상이 활용된다. 예를 들어, 2개의 큐비트가 얽혀있으면, 4가지 가능한 상태를 갖는 단일객체로 생각할 수 있다. 다음 그림은 두 큐비트의 서로 다른 조합에 해당하는 4가지 상태 (0, 0), (0, 1), (1, 0), (1, 1)의 퍼텐셜을 보여준다. 각 상태의 상대적인 에너지는 큐비트 Bias와 큐비트 사이의 Coupling에 따라 달라진다.
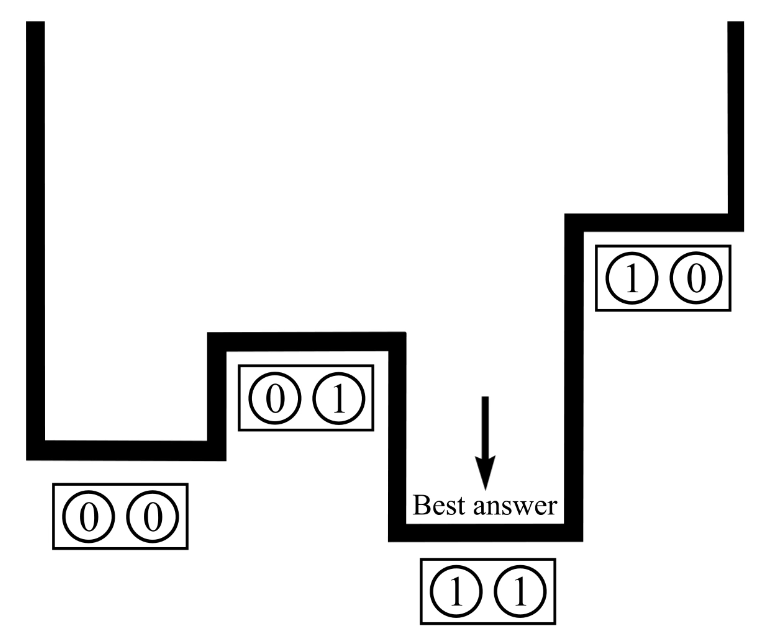
각 큐비트에는 Bias가 있으며, 큐비트는 Coupler를 통해 상호작용한다. 문제를 공식화할 때, 사용자는 Bias 및 Coupler 값을 선택한다. Bias와 Coupling은 목적함수의 에너지 지형(Energy Landscape)를 정의하고, D-Wave 양자컴퓨터는 해당 지형의 최소에너지를 샘플링 기반으로 탐색한다. 이것이 양자어닐링의 개요이다.
당연한 말이지만 큐비트가 추가될수록 시스템은 점점 더 복잡해진다. 2개의 큐비트는 에너지 환경을 4가지 가능한 상태로 정의한다. 3개의 큐비트는 8가지 상태를 갖는다. 매번 추가되는 큐비트는 에너지 환경을 정의하는 상태공간의 수를 2배씩 증가시킨다. 결국 상태의 수는 큐비트 수에 따라 기하급수적으로 증가하게 된다.
정리하자면 다음과 같다.
- 시스템은 각각 0과 1의 중첩상태에 있는 큐비트 집합으로 시작한다. 아직 결합되어 있지 않다.
- 양자어닐링이 시작되면 Bias와 Coupler가 도입되고 큐비트는 얽히게 된다. 이 시점에서 시스템은 많은 해가 얽힌 추상적인 양자상태에 있다.
- 어닐링이 끝날 때까지 각 큐비트는 문제의 최소에너지 상태 또는 매우 가까운 상태를 나타내는 고전적인 상태로 붕괴한다.
- 이 모든 과정은 D-Wave 양자컴퓨터에서 마이크로초 단위로 발생한다.
Underlying Quantum Physics
이제 D-Wave 양자어닐링을 이해하는데 필요한 몇가지 물리적 개념에 대해 알아보자.
The Hamiltonian and The Eigenspectrum
고전적인 해밀토니안은 에너지 관점에서 일부 물리적 시스템의 수학적 설명이다. 우리는 시스템의 특정 상태를 입력할 수 있고, 해밀토니안은 해당 상태에 대한 에너지를 반환한다. 대부분의 볼록하지 않은(Non-convex) 해밀토니안에 대한 최소에너지 상태를 찾는 것은 고전적인 컴퓨터가 효율적으로 풀 수 없는 NP-Hard 문제이다.
고전적인 시스템의 예시로 테이블과 사과가 있는 매우 단순한 시스템을 생각하자. 이 시스템에는 2가지 가능한 상태가 있다. 테이블 위에 있는 사과와 테이블 아래에 있는 사과이다. 해밀토니안은 에너지를 알려준다. 이를 통해 사과가 테이블 아래에 있을 때보다 테이블 위에 있는 상태가 더 높은 에너지를 갖고 있음을 구별할 수 있다.
양자시스템의 경우 해밀토니안은 고유상태(Eigenstate)라고 하는 특정 상태를 에너지에 매핑하는 함수이다. 시스템이 해밀토니안의 고유상태에 있을 때만 시스템의 에너지가 잘 정의되고, 이를 고유에너지(Eigenenergy)라고 한다. 시스템이 다른 상태에 있을 때 에너지는 불확실하다. 정의된 고유에너지가 있는 고유상태의 집합은 고유스펙트럼(Eigenspectrum)을 구성한다.
D-Wave 양자컴퓨터의 경우, 해밀토니안은 다음과 같이 표현된다.
$$ {\cal H}{ising} = \underbrace{- \frac{A({s})}{2} \left(\sum_i {\hat\sigma{x}^{(i)}}\right)}\text{Initial Hamiltonian} + \underbrace{\frac{B({s})}{2} \left(\sum{i} h_i {\hat\sigma_{z}^{(i)}} + \sum_{i>j} J_{i,j} {\hat\sigma_{z}^{(i)}} {\hat\sigma_{z}^{(j)}}\right)}_\text{Final Hamiltonian} $$
여기서 ${\hat\sigma_{x,z}^{(i)}}$는 하나의 큐비트 $q_i$에 작용하는 Pauli 행렬이고, $h_i$와 $J_{i,j}$는 큐비트의 bias와 coupling strength이다. $h_i$와 $J_{i, j}$의 0이 아닌 값(Nonzero value)는 작업 그래프(Working Graph) 안에서 사용가능한 것으로 한정된다.
전체 해밀토니안은 초기 해밀토니안(Initial Hamiltonian)과 최종 해밀토니안(Final Hamiltonian) 두 항의 합이다. 열통계물리학을 공부한 사람이라면, 위 수식이 외부자기장이 존재할 때의 고전적인 Ising model의 해밀토니안과 유사하다는 것을 알 수 있을 것이다.
- 초기 해밀토니안 (첫번째 항) : 초기 해밀토니안의 가장 낮은 에너지 상태는 모든 큐비트가 0과 1의 중첩상태에 있을 때이다. 이 항은 터널링(Tunneling) 해밀토니안이라고도 한다.
- 최종 해밀토니안 (두번째 항) : 최종 해밀토니안의 가장 낮은 에너지 상태는 해결하려는 문제에 대한 답이다. 최종 상태는 고전적인 상태이며, 큐비트 bias와 큐비트 간의 커플링을 포함한다. 이 항은 문제(Problem) 해밀토니안이라고도 한다.
양자어닐링에서 시스템은 초기 해밀토니안의 가장 낮은 에너지 고유상태에서 시작된다. 어닐링되면서 Bias와 Coupler를 포함하는 Problem Hamiltonian을 도입하고, Initial Hamiltonian의 영향을 줄인다. 어닐링이 끝나면 Problem Hamiltonian의 고유상태가 된다.
이상적으로는 양자어닐링 프로세스 전반에 걸쳐 최소 에너지 상태를 유지하여 결국 Problem Hamiltonian의 최소에너지 상태에 있게 되므로 해결하려는 문제에 대한 답을 얻게 된다. 어닐링이 끝나면 각 큐비트는 고전적인 객체로 돌아간다.
Annealing in Low-Energy States
양자어닐링 과정을 시각화하기 위해 Eigenenergies vs Time 그림을 보는 것이 효과적이다. 어닐링 중 가장 낮은 에너지 상태인 바닥상태(Ground State)는 일반적으로 가장 아래에 표시되고, 더 높은 여기상태(Excited State)는 그 위에 표시된다. 다음 그림을 참고하자.
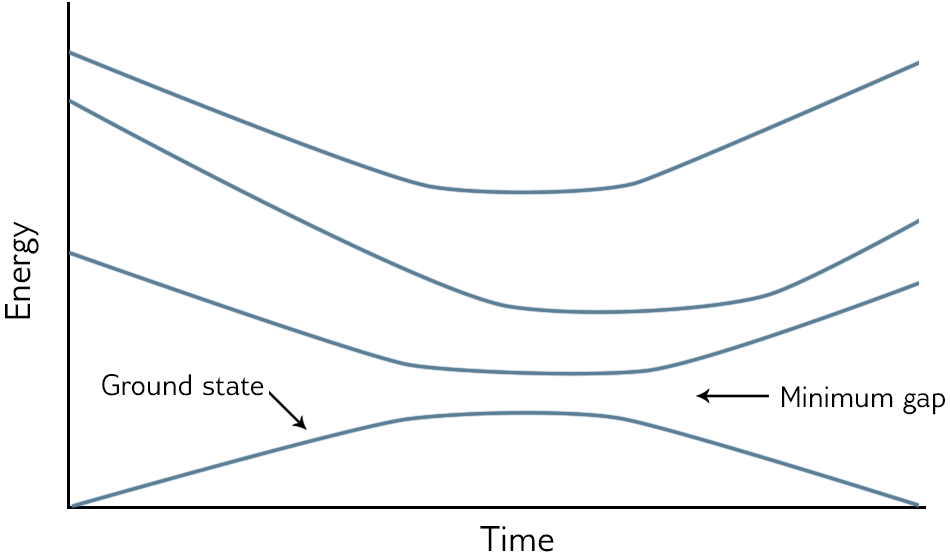
어닐링이 시작되면 시스템은 다른 에너지 레벨과 잘 분리된 가장 낮은 에너지 상태에서 시작한다. Problem Hamiltonian가 도입됨에 따라 다른 에너지 준위가 바닥상태에 가까워질 수 있다. 두 에너지 준위가 가까울수록 시스템이 가장 낮은 에너지 상태에서 여기상태 중 하나로 점프할 확률이 높아진다. 어닐링 동안 바닥상태에서 가장 낮은 에너지를 갖는 첫번째 여기상태가 바닥상태에 가깝게 접근한 다음 다시 발산하는 특정한 지점이 있다. 어닐링의 모든 지점에서 바닥상태와 첫번째 여기상태 사이의 최소거리를 최소간격(Minimum Gap)이라고 한다.
특정 요인으로 인해 시스템이 바닥상태에서 더 높은 에너지 상태로 점프할 수 있다. 원인 중 하나는 모든 물리적 시스템에 존재하는 열적 변동(Thermal Fluctuation)이고, 다른 하나는 어닐링 과정을 매우 빠르게 실행하는 것이다.
외부 에너지원의 간섭을 받지 않고 충분히 느리게 해밀토니안을 변화시키는 어닐링 과정을 단열과정(Adiabatic Process)라고 하며, 여기서 단열 양자컴퓨팅(Adiabatic Quantum Computing)이라는 이름이 유래했다. 실제 계산은 완벽하게 격리되어 실행될 수 없기 때문에, 양자어닐링은 이론적 이상인 단열양자 컴퓨팅의 현실적인 대응물로 생각할 수 있다. 일부 문제의 경우 바닥상태에 머무를 확률이 때때로 낮을 수 있지만, 반환되는 낮은 에너지 상태는 여전히 유용하다.
모든 문제는 각각 다른 해밀토니안과 고유스펙트럼이 존재한다. 양자어닐링의 관점에서 가장 어려운 문제는 일반적으로 최소간격이 가장 작은 문제이다.
Evolution of Energy States
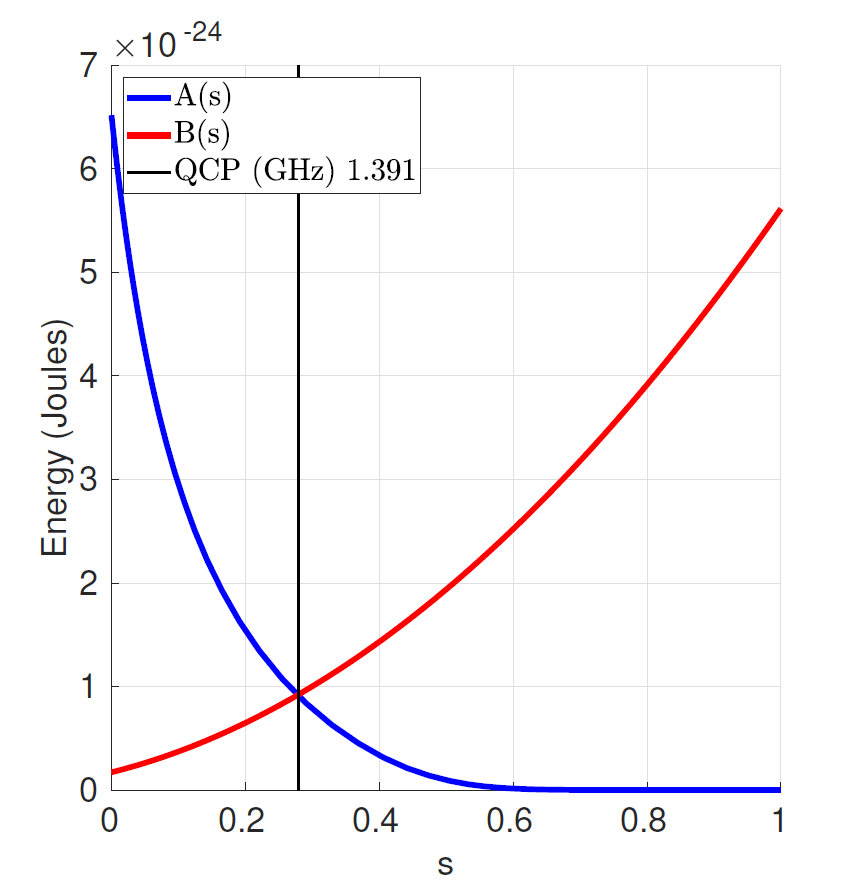
아래의 그림은 $s$에서의 해밀토니안 안의 파라미터 $A$, $B$에 대한 의존성(Dependence), 정규화된 어닐링 비율(Normalized Anneal Fraction), 0과 1 사이의 추상매개변수(Abstract Parameter)를 보여준다.
$A(s)$ 곡선은 터널링 에너지(Tunneling Energy)이고, $B(s)$ 곡선은 Problem Hamiltonian Energy이며 모두 줄(Joules) 단위로 표시된다.
선형 어닐링 집합 $s = t / t_f$에서 $t$는 시간이고, $t_f$는 어닐링의 총 시간이다. $t = 0, A(0) >> B(0)$일 때, 시스템은 각 스핀이 고전상태의 비편재화된 조합(delocalized combination)에 있는 시스템의 양자 바닥상태에 있다. 시스템이 어닐링됨에 따라 A는 감소하고, B는 $t_f$까지 증가한다.
어닐링이 끝나면 해밀토니안은 유일한 B(s) 항을 포함한다. 가능한 모든 고전적인 Bitstring(0 또는 1의 큐비트 상태목록)은 고유상태에 해당하고, 시스템에 입력했던 고전적 해밀토니안이 고유 에너지가 된다.
이렇게 해서 지금까지 기초적인(?) Quantum Annealing 배경지식에 대해 알아보았다. 그럼 이것으로 무엇을 할 수 있을까? 여러가지 NP-Hard 문제를 이차함수와 그래프 구조로 제대로 변환할 수 있다면, 고전적인 최적화 알고리즘에 더 좋은 성과를 얻을 수 있다고 D-Wave에서 주장하고 있다.
D-Wave에서는 양자어닐링을 활용할 수 있는 여러가지 예제를 제공하고 있는데, 그 중 하나인 TSP에 대해 알아보자!
4 Traveling Salesman Problem (TSP)
여행하는 외판원 문제 (Traveling Salesman Problem, TSP)는 조합최적화(Combinatorial Optimization) 분야에서 잘 알려진 NP-Hard 문제이다. 이 문제는 여러 도시의 목록과 각 도시 사이의 거리가 주어진 상태에서 정확히 1번씩 각 도시를 방문하는 최소비용경로를 요구한다.
Methods
가장 먼저 떠올릴 수 있는 방법은 Brute-Force Search를 이용하여 모든 수열(Permutation, 순서가 있는 조합)을 시도하고, 어느 경로가 가장 낮은 비용에 대응되는가를 확인하는 것이다. 그러나 이런 방법의 실행시간(Running Time)을 고려하면 문제가 쉽지 않다는 것을 깨닫게 된다. 도시의 수를 $N$이라 할 때, 알고리즘의 시간복잡도는 $O(N!)$으로 표현될 것이기 때문이다. 따라서 도시의 수 $N$이 20개만 되어도 이는 실용적이지 않은 방법이 된다. 다행히 많은 휴리스틱 알고리즘들이 알려져 있고, 수만개의 도시를 가진 일부 사례들은 완벽하게 계산될 수 있다.
여기서는 TSP의 작은 예시를 D-Wave를 이용하여 풀어볼 것이다. 두 종류의 Annealing을 사용할 것인데, 하나는 Simulated Annealing이고, 다른 하나는 D-Wave Advantage QPU 위에서 작동하는 Quantum Annealing이다.
TSP as graph problem
TSP에서 우리가 구하고자 하는 정답은 가중치화된 그래프의 노드로 구성된 특정한 순서배열이라고 생각할 수 있다. 방향성이 없는 가중치 그래프(Undirected Weighted Graph)를 가진 상태에서, 각 도시는 그래프의 노드에 대응되고, 두 도시 사이의 경로는 엣지에 대응되며, 한 경로의 거리는 엣지의 가중치가 될 수 있다.
또한 이 문제에서 우리는 모든 도시 사이의 가능한 모든 경로를 고려한다고 가정한다. 즉, 임의의 두 노드의 쌍은 언제나 하나의 엣지로 연결되어 있다고 보는데, 이러한 그래프는 완전(Complete)하다고 한다. 만약 두 도시 사이의 연결이 존재하지 않는다면, 그래프를 완전하게 만들기 위해 최적해에 영향을 주지 않는 엣지 하나를 임의로 추가할 수 있다.
결국 TSP의 목표는 이러한 완전그래프가 주어진 상황에서 최소한의 가중치를 갖는 Hamiltonian Cycle을 찾는 것이라고 할 수 있다.
Binary Encoding
(Quantum) Annealing으로 TSP를 풀기 위해서는 TSP를 일반적인 Quadratic Unconditioned Binary Optimization (QUBO) 형식으로 수식화해야 한다. QUBO 형식은 다음과 같이 표현된다.
$$ \mathrm{min} \hspace{0.1cm} y=x^{\intercal}Qx + x^{\intercal}B + c $$
여기서 $x = (x_{1}, x_{2}, \dots)$는 이진결정변수(Binary-Decision Variables) $x_{i} = 0, 1$의 벡터이다.
편의상 이중인덱스 이진변수(Double-Indexed Binary Variable)을 도입한다. $i$-index 도시가 Cycle의 $j$ 위치에 있다면, $x_{i, j} = 1$이고, 아니면 0이라고 정의한다. 예를 들면 뉴욕, 로스엔젤레스, 시카고 3개의 도시가 있다고 하자. 도시의 인덱스를 지정해야 하는데, 뉴욕을 0, 로스엔젤레스를 1, 시카고를 2로 표현하자. 그러면 $x_{0, 0} = x_{1, 2} = x_{2, 1} = 1$은 우리가 이 도시들을 뉴욕 $\rightarrow$ 시카고 $\rightarrow$ 로스엔젤레스 순서로 방문함을 의미한다.
최종적으로 다음과 같은 목적함수가 설명하는, 가장 짧은 길이를 갖는 Hamiltonian Cycle을 찾는 것이 목표가 된다.
$$ H_{\mathrm{dist}} = \sum_{i,j} D_{i,j} \sum_{k} x_{i,k}x_{j,k+1} $$
여기서 $D_{i, j}$는 도시 $i$와 도시 $j$ 사이의 거리이다. 주목해야 할 것은 도시 $i$가 사이클의 $k$ 위치에 있고, 도시 $j$가 사이클의 그 다음 위치에 있을 때만 $x_{i, k} x_{j, k+1} = 1$이 성립된다는 것이다. 이 경우 우리는 거리 $D_{i, j}$를 최소화의 대상인 목적함수에 더해서 연속된 도시들 사이의 거리의 전체비용을 모두 더하게 된다.
마지막으로 최적화 문제의 2가지 제한조건(Constraints)이 명시되어야 한다.
- 각 도시는 사이클 상에 정확히 1번 등장해야 한다.
$$ \sum_{j=0}^{N-1} x_{i,j}=1 \hspace{0.5cm} \forall i=0,...,N-1 $$ - 사이클 상의 각 위치는 정확히 하나의 도시에 할당되어야 한다.
$$ \sum_{i=0}^{N-1} x_{i,j}=1 \hspace{0.5cm} \forall j=0,...,N-1 $$
예를 들면, 도시의 수 $N = 4$인 경우의 경로 $[1, 3, 2, 4]$는 다음 표와 같이 표현될 수 있다. 각 행과 열의 총합이 1이라는 것은 제한조건을 잘 지키는 경로임을 의미한다.

최적화 과정에서 제한조건을 잘 만족하는 해의 탐색을 강화하려면, 다음과 같은 페널티 항을 목적함수에 더해주는 것이 효과적이다.
$$ H_{\mathrm{constraint}} = P \sum_{i=0}^{N-1} \left(1-\sum_{j=0}^{N-1} x_{i,j}\right)^{2} + P \sum_{j=0}^{N-1} \left(1-\sum_{i=0}^{N-1} x_{i,j}\right)^{2} $$
페널티 항에 의해 모든 도시가 사이클의 일부로 정확히 1번만 방문되어야 한다는 조건이 강화된다. 만약 제한조건이 성립되지 않을 경우, 높은 페널티항 $P$가 목적함수에 더해지고 이는 최소화 과정에서 자연스럽게 배제될 것이다. 여기서는 편의상 동일한 페널티 항 $P$를 두 종류의 제한조건에 공통적으로 사용하였다.
결국 전체 해밀토니안은 다음과 같이 표현된다.
$$ H = H_{\mathrm{dist}} + H_{\mathrm{constraint}} $$
여기서 페널티 항 $P$는 머신러닝에서의 하이퍼파라미터와 같다. 그러므로 제한조건을 따르는 최적해를 찾기 위해, $P$에 대한 Hyperparameter Optimization을 수행해야 한다. 만약 $P$가 적절하게 선택되지 않는다면 최적화 알고리즘은 이상한 해를 제공할 수도 있다. 예를 들면 모든 도시를 애초에 방문하지 않거나, 특정 도시를 여러 번 방문하는 루트를 제공할 수도 있다.
Libraries
지금까지 설명한 내용을 실제로 구현한 코드를 알아보자. D-Wave에서 제공하는 예제 코드를 기반으로 하였으나, 공부를 하는 과정에서 유사 데이터 생성, 클러스터링 적용, Folium 라이브러리를 활용한 최적루트 시각화 등이 추가되었다.
import boto3
from braket.aws import AwsDevice
from braket.ocean_plugin import BraketSampler, BraketDWaveSampler
from sklearn.preprocessing import MaxAbsScaler, MinMaxScaler, StandardScaler, LabelEncoder
import math
import numpy as np
import pandas as pd
import networkx as nx
import dimod
import dwave_networkx as dnx
from dimod.binary_quadratic_model import BinaryQuadraticModel
from dwave.system.composites import EmbeddingComposite
import matplotlib.pyplot as plt
%matplotlib inline
from collections import defaultdict
from tqdm import tqdm
import itertools
from utils_tsp import get_distance, traveling_salesperson
from sklearn import cluster, mixture, datasets
from sklearn.preprocessing import StandardScaler
import plotly.io as pio
import plotly.express as px
import plotly.graph_objects as go
import plotly.figure_factory as ff
from plotly.subplots import make_subplots
from plotly.validators.scatter.marker import SymbolValidator
import folium
from folium import plugins
from folium.plugins import *
from haversine import haversine
%load_ext autoreload
%autoreload 2
# Fix random seed for reproducibility
seed = 1234
np.random.seed(seed)
# Please enter the S3 bucket you created during onboarding in the code below
my_bucket = "amazon-braket-90e46b3eeef2" # the name of the bucket
my_prefix = "Amadeus-System-Dwave/" # the name of the folder in the bucket
s3_folder = (my_bucket, my_prefix)
print(s3_folder)
Generation of Synthetic Data
다음과 같이 일정량의 배송주문이 들어온다고 가정하고, 이를 표현하기 위한 유사 데이터를 생성하였다.
x_left = 37.53916
x_right = 37.55222
y_high = 127.04727
y_low = 127.05551
num_samples = 400
products = {'컴퓨터': 0, '마우스': 0, '키보드': 0, '도서': 0, '펜': 0, '연필': 0, '필통': 0, '유리컵': 0, '공책': 0,
'채소': 1, '커피': 1, '녹차': 1, '무': 1,
'쇠고기': 2, '돼지고기': 2, '닭고기': 2, '생선': 2, '김치': 2, '젓갈': 2, '피자': 2, '아이스크림': 2, '얼음': 2}
rdf = pd.DataFrame()
rdf['city'] = list(range(num_samples))
rdf['x'] = np.random.uniform(low = x_left, high = x_right, size = num_samples)
rdf['y'] = np.random.uniform(low = y_low, high = y_high, size = num_samples)
rdf['product'] = np.random.choice(list(products.keys()), size = num_samples)
rdf['freshness'] = np.random.choice(list(products.values()), size = num_samples)
rdf['quantities'] = np.random.randint(50, size = num_samples)
rdf
Clustering
$N$개의 주문배송 건은 $N$개의 배송지에 대응되므로, 이를 그래프로 그대로 변환하면 매우 복잡한 그래프가 될 것이다. 따라서 데이터의 주문 특성을 기반으로 클러스터링 알고리즘을 적용하였다.
클러스터링 알고리즘은 Sklearn에서 제공하는 여러 모듈을 활용하였으며, 각각의 클러스터링 알고리즘은 세부적인 특성이 조금씩 다르다. 예를 들면, K-means Clustering은 클러스터의 수 $K$를 사용자가 지정해주어야 한다. 그러나 DBSCAN 알고리즘은 밀도추정(Density Estimation) 기반으로 작동하므로 사용자의 의지와 무관하게 알고리즘이 스스로 적절한 클러스터의 수를 지정한다.
num_clusters = 8
random_state = 1234
kmeans = cluster.KMeans(n_clusters = num_clusters, random_state = random_state)
minibatch_kmeans = cluster.MiniBatchKMeans(n_clusters = num_clusters, random_state = random_state)
affinity_propagation = cluster.AffinityPropagation(damping = 0.9, preference = -200)
spectral_clustering = cluster.SpectralClustering(n_clusters = num_clusters, random_state = random_state)
hierarchical_clustering = cluster.AgglomerativeClustering(n_clusters = num_clusters, linkage = 'ward')
dbscan = cluster.DBSCAN(eps = 0.3)
models = {'kmeans' : kmeans,
'mini_kmeans' : minibatch_kmeans,
'affine' : affinity_propagation, # 클러스터 수 자동 생성
'spectral' : spectral_clustering,
'hierarchical' : hierarchical_clustering,
'dbscan' : dbscan} # 클러스터 수 자동 생성
X = np.array(rdf[['x', 'y', 'freshness', 'quantities']]) # 클러스터링 학습 특성
model = models['kmeans']
model.fit(X)
if hasattr(model, 'labels_'):
print('1')
labels = model.labels_.astype(np.int)
else:
print('2')
labels = model.predict(X)
colors = np.array(['red', 'blue', 'green', 'violet', 'black', 'yellow', 'purple', 'white', 'darkblue'])
rdf['label'] = labels # DataFrame
rdf['color'] = colors[labels] # DataFrame
fig = px.scatter(rdf, x = 'x', y = 'y', color = 'color', size = 'quantities', opacity = 0.5,
title = 'Visualization of Clustering')
fig.show()
print('Labels : {}'.format(model.labels_))
print('Inertia : {}'.format(model.inertia_))
print('Number of Iterations : {}'.format(model.n_iter_))
print('Number of Features : {}'.format(model.n_features_in_))
print('Center of Each Clustering :\n', model.cluster_centers_)
rdf
Labels : [2 1 7 1 7 4 4 3 4 5 1 6 0 3 0 0 4 0 1 3 7 2 0 5 1 2 3 2 7 0 5 3 7 5 3 4 1
4 0 3 0 3 7 2 1 1 2 6 4 7 5 3 3 6 1 0 1 1 6 6 0 2 5 1 2 0 0 1 4 0 0 6 3 4
0 5 7 2 3 0 1 4 3 1 2 0 3 3 2 5 6 6 1 5 3 0 5 3 5 5 5 5 7 5 0 5 2 7 5 3 3
0 5 3 3 5 2 2 7 3 0 4 0 3 7 6 6 5 2 4 4 1 6 7 2 6 6 7 6 2 0 2 4 7 6 0 2 3
5 3 4 5 2 5 7 4 7 0 3 7 3 0 2 3 7 3 0 7 1 6 0 0 2 1 2 5 2 3 3 2 6 0 3 3 1
2 6 4 4 6 5 2 7 6 0 4 2 1 0 1 2 5 7 3 0 5 5 5 0 2 2 2 6 1 1 1 3 4 1 0 2 5
1 0 0 7 1 0 1 3 5 2 3 7 6 1 2 6 5 0 1 4 6 5 5 0 2 3 1 0 6 4 6 1 1 7 3 3 3
4 3 6 4 4 7 5 7 1 7 3 1 0 3 3 1 3 6 0 5 2 2 7 3 3 1 1 1 5 2 3 4 5 5 5 4 7
3 0 7 5 5 3 3 1 0 6 3 3 6 6 1 0 3 1 3 4 1 4 0 0 6 3 0 6 1 3 7 1 2 3 3 1 6
7 5 5 3 1 4 0 2 7 1 0 6 0 4 1 5 5 4 2 5 4 2 3 7 4 1 2 2 4 5 2 7 0 4 4 0 2
4 1 4 2 5 7 0 5 3 7 5 2 6 7 7 0 4 5 7 6 6 6 7 1 3 5 5 7 3 6]
Inertia : 1426.9490441813796
Number of Iterations : 3
Number of Features : 4
Center of Each Clustering :
[[ 37.54567581 127.05126879 1.08928571 3.46428571]
[ 37.54635973 127.05156157 0.8490566 36.03773585]
[ 37.54482789 127.05131257 0.97959184 22.16326531]
[ 37.54646633 127.05174457 1.29230769 42.90769231]
[ 37.54592159 127.05112287 0.975 15.375 ]
[ 37.5455591 127.05133747 0.92592593 29.14814815]
[ 37.54614436 127.05132432 1.025 9.65 ]
[ 37.54688686 127.05185179 1.06976744 47.6744186 ]]위 결과에서 마지막 8개의 좌표는 클러스터링 알고리즘이 계산한 클러스터의 중심좌표이다. 각각의 클러스터를 하나의 노드로 표현할 것이므로, 각 클러스터의 중심좌표는 노드의 위치정보가 된다.
Distance Matrix
클러스터의 각 중심좌표는 위도, 경도의 좌표로 표현되어 있었으므로 이를 실제 지도 상황에 맞게 km 단위로 계산해야 한다. 아래 코드에서 사용된 haversine 함수는 위도, 경도, 단위를 지정하면 거리를 반환한다.
distances = pd.DataFrame(index = list(range(len(set(model.labels_)))),
columns = list(range(len(set(model.labels_)))))
# Fill Distance between clustering centers
for i in center_df['center']:
for j in center_df['center']:
i_coords = [center_df.loc[i]['x'], center_df.loc[i]['y']]
j_coords = [center_df.loc[j]['x'], center_df.loc[j]['y']]
distance = haversine(i_coords, j_coords, unit = 'km')
distances.loc[i][j] = round(distance, 2)
distances
Set up Graph
이제 노드 사이의 모든 거리정보를 테이블로 얻었으니 이를 그래프 구조로 변환할 수 있다. 네트워크 분석에 자주 활용되는 Python 라이브러리인 NetworkX를 사용하였다.
G = nx.from_pandas_adjacency(df) # Graph object created from distance matrix
pos = nx.spring_layout(G, seed = seed) # Node Coordinates auto-generated
nodes = G.nodes()
edges = G.edges()
weights = nx.get_edge_attributes(G, 'weight', )
print('Number of nodes : {}'.format(G.number_of_nodes()))
print('Nodes of Graph : {}'.format(nodes))
print('Number of edges : {}'.format(G.number_of_edges()))
print('Edges of Graph : {}'.format(edges))
print('Weights of Graph : {}'.format(weights))
# Show Graph with weights
plt.figure(figsize = (10, 10))
plt.axis('off')
nx.draw_networkx(G, pos, with_labels = True);
nx.draw_networkx_edge_labels(G, pos, edge_labels = weights, alpha = 0.8);
QUBO for TSP
그래프 정보를 QUBO 형식으로 수식화하고, 적절한 페널티 항 $P$ 값을 찾기 위해 탐색범위를 지정한다.
tsp_qubo = dnx.algorithms.tsp.traveling_salesman_qubo(G) # QUBO Transform for TSP
lagrange = None # Default Langrange Parameter for enforcing constraints
weight = 'weight'
N = G.number_of_nodes()
if lagrange is None:
if G.number_of_edges() > 0:
# Default lagrange Parameter
lagrange = G.size(weight = weight) * G.number_of_nodes() / G.number_of_edges()
else:
lagrange = 2
print('Default Lagrange Parameter : {}'.format(lagrange))
# Generate Parameter list for Hyperparameter Optimization
lagrange_list = list(np.arange( int(0.75 * lagrange), int(1.5 * lagrange), step = 0.1 * lagrange )) # between 75% ~ 150%
print('Number of Lagrange Parameters : {}'.format(len(lagrange_list)))
print('Lagrange Parameter for HPO : {}'.format(lagrange_list))
Classical Simulated Annealing
먼저 고전적인 Simulated Annealing으로 계산을 시도하였다.
%%time
sampler = dimod.SimulatedAnnealingSampler() # Classical Simulated Annealing
route = dnx.traveling_salesman(G, sampler, start = 0) # Start with city-0 / sampler 대신 dimod.ExactSolver() 가능
print('Route found with Simulated Annealing : {}'.format(route))
# Total Distance
total_distance = 0
for idx, node in enumerate(route[:-1]):
distance = df[route[idx + 1]][route[idx]]
total_distance += distance
print('Total Distance (without return) : {}'.format(total_distance))
# Add Distance between start and end point to complete cycle
return_distance = df[route[0]][route[-1]]
print('Distance between start and end : {}'.format(return_distance))
# Distance for full cycle
full_distance = total_distance + return_distance
print('Total Distance (including return) : {} \n'.format(full_distance))Route found with Simulated Annealing : [0, 5, 7, 1, 3, 6, 4, 2]
Total Distance (without return) : 0.43999999999999995
Distance between start and end : 0.09
Total Distance (including return) : 0.5299999999999999
CPU times: user 8.92 s, sys: 0 ns, total: 8.92 s
Wall time: 8.92 s
Quantum Annealing on D-Wave with HPO for Lagrange Parameter
이제 Quantum Annealing으로 계산해보자. 최적 계산을 위해 Hyperparameter Optimization을 함께 하였다.
%%time
# run TSP with imported TSP routine
sampler = BraketDWaveSampler(s3_folder ,device_arn='arn:aws:braket:::device/qpu/d-wave/Advantage_system4') # more big Advantage Chip
sampler = EmbeddingComposite(sampler)
# Set Parameters
num_shots = 100
start_city = 0
best_distance = sum(weights.values())
best_route = [None] * len(G)
# Searching Optimal Route / Hyperparameter Optimization
for lagrange in tqdm(lagrange_list):
print('Running Quantum Annealing for TSP with Lagrange Parameter = {}'.format(lagrange))
route = traveling_salesperson(G, sampler, lagrange = lagrange,
start = start_city, num_reads = num_shots, answer_mode = 'histogram')
# Print Route
print('Route found with D-Wave : {}'.format(route))
# print Distance
total_distance, distance_with_return = get_distance(route, df)
# Update best values
if distance_with_return < best_distance:
best_distance = distance_with_return
best_route = route
print()
print('===== Final Solution =====')
print('Best Solution found with D-Wave : {}'.format(best_route))
print('Total Distance (including return) : {}'.format(best_distance)) 0%| | 0/14 [00:00<?, ?it/s]
Running Quantum Annealing for TSP with Lagrange Parameter = 0.0
7%|▋ | 1/14 [00:24<05:21, 24.77s/it]
Route found with D-Wave : [0, 1, 7, 6, 5, 4, 3, 2]
Total distance (without return): 0.6100000000000001
Total distance (including return): 0.7000000000000001
Running Quantum Annealing for TSP with Lagrange Parameter = 0.07142857142857144
14%|█▍ | 2/14 [00:52<05:21, 26.77s/it]
Route found with D-Wave : [0, 5, 1, 4, 6, 3, 7, 2]
Total distance (without return): 0.52
Total distance (including return): 0.61
Running Quantum Annealing for TSP with Lagrange Parameter = 0.14285714285714288
21%|██▏ | 3/14 [01:10<04:06, 22.39s/it]
Route found with D-Wave : [0, 2, 7, 5, 3, 1, 6, 4]
Total distance (without return): 0.66
Total distance (including return): 0.6900000000000001
Running Quantum Annealing for TSP with Lagrange Parameter = 0.2142857142857143
29%|██▊ | 4/14 [01:32<03:42, 22.22s/it]
Route found with D-Wave : [0, 3, 6, 5, 4, 2, 7, 1]
Total distance (without return): 0.6699999999999999
Total distance (including return): 0.7499999999999999
Running Quantum Annealing for TSP with Lagrange Parameter = 0.28571428571428575
36%|███▌ | 5/14 [01:49<03:04, 20.49s/it]
Route found with D-Wave : [0, 6, 3, 7, 4, 2, 1, 5]
Total distance (without return): 0.66
Total distance (including return): 0.67
Running Quantum Annealing for TSP with Lagrange Parameter = 0.3571428571428572
43%|████▎ | 6/14 [02:10<02:44, 20.50s/it]
Route found with D-Wave : [0, 3, 7, 6, 4, 1, 5, 2]
Total distance (without return): 0.5
Total distance (including return): 0.59
Running Quantum Annealing for TSP with Lagrange Parameter = 0.4285714285714286
50%|█████ | 7/14 [02:36<02:37, 22.55s/it]
Route found with D-Wave : [0, 6, 4, 2, 1, 7, 5, 3]
Total distance (without return): 0.69
Total distance (including return): 0.7899999999999999
Running Quantum Annealing for TSP with Lagrange Parameter = 0.5000000000000001
57%|█████▋ | 8/14 [03:12<02:41, 26.88s/it]
Route found with D-Wave : [0, 4, 2, 1, 7, 3, 5, 6]
Total distance (without return): 0.6100000000000001
Total distance (including return): 0.6600000000000001
Running Quantum Annealing for TSP with Lagrange Parameter = 0.5714285714285715
64%|██████▍ | 9/14 [03:35<02:07, 25.53s/it]
Route found with D-Wave : [0, 7, 1, 2, 3, 4, 5, 6]
Total distance (without return): 0.75
Total distance (including return): 0.8
Running Quantum Annealing for TSP with Lagrange Parameter = 0.6428571428571429
71%|███████▏ | 10/14 [04:11<01:55, 28.75s/it]
Route found with D-Wave : [0, 7, 6, 3, 4, 5, 2, 1]
Total distance (without return): 0.65
Total distance (including return): 0.73
Running Quantum Annealing for TSP with Lagrange Parameter = 0.7142857142857144
79%|███████▊ | 11/14 [04:38<01:24, 28.24s/it]
Route found with D-Wave : [0, 2, 5, 7, 3, 6, 1, 4]
Total distance (without return): 0.51
Total distance (including return): 0.54
Running Quantum Annealing for TSP with Lagrange Parameter = 0.7857142857142858
86%|████████▌ | 12/14 [05:03<00:54, 27.22s/it]
Route found with D-Wave : [0, 4, 1, 7, 3, 5, 2, 6]
Total distance (without return): 0.54
Total distance (including return): 0.5900000000000001
Running Quantum Annealing for TSP with Lagrange Parameter = 0.8571428571428572
93%|█████████▎| 13/14 [05:32<00:27, 27.73s/it]
Route found with D-Wave : [0, 4, 5, 6, 7, 3, 1, 2]
Total distance (without return): 0.4700000000000001
Total distance (including return): 0.56
Running Quantum Annealing for TSP with Lagrange Parameter = 0.9285714285714287
100%|██████████| 14/14 [05:53<00:00, 25.22s/it]
Route found with D-Wave : [0, 7, 3, 2, 4, 5, 6, 1]
Total distance (without return): 0.6400000000000001
Total distance (including return): 0.7200000000000001
===== Final Solution =====
Best Solution found with D-Wave : [0, 2, 5, 7, 3, 6, 1, 4]
Total Distance (including return) : 0.54
CPU times: user 3min 54s, sys: 633 ms, total: 3min 55s
Wall time: 5min 57s위 결과를 보면, 페널티 항 $P$에 따라 목적함수의 값이 감소하는 정도가 확연히 다름을 알 수 있다.
Meta-Optimized Route
이제 최적화된 경로를 시각화해보자.
# Mapping from original nodes to position in cycle
node_labels = {list(nodes)[ii] : best_route[ii] for ii in range(num_cities)}
print(node_labels)
# Construct Route as a list of (node_i, node_i+1)
sol_graph_base = [ (best_route[idx], best_route[idx + 1]) for idx in range(len(best_route) - 1)]
# Establish weights between nodes along route, allowing for mirrored keys (weights[(0, 1)] = weights[(1, 0)])
best_weights = {k : weights[k] if k in weights.keys() else weights[(k[1], k[0])] for k in sol_graph_base}
# Rebuild Graph containing only Route Connections
G_best = nx.Graph(sol_graph_base)
route_labels = {x : f'step_{i} = {best_weights[x]}' for i, x in enumerate(sol_graph_base)}
# Show Solution
plt.figure(figsize = (10, 10))
plt.axis('off');
nx.draw_networkx(G_best, pos, font_color = 'w');
nx.draw_networkx_edge_labels(G_best, pos, edge_labels = route_labels, label_pos = 0.25);

여기서 각 노드의 좌표정보는 그래프 표현을 위해 임의로 설정된 것이다. NetworkX의 spring_layout()을 활용하였다. 결과적으로 8개의 클러스터 노드에 대한 최소비용경로를 D-Wave Quantum Annealing으로 최적화할 수 있었다.
Visualization of Meta-Optimized Route using Folium
최적루트 연산이 종료된 시점에서 복잡한 것은 더 이상 없었다. 그런데 그냥 끝내기에는 조금 심심해서 예전에 배웠던 Folium 라이브러리를 활용해보았다.
Folium 라이브러리는 Python에서 지도와 관련된 여러 기능을 제공한다. 예를 들면, 지도의 확대 및 축소, 미니맵, 풍량 및 풍향 표현 뿐만 아니라 Interactive한 좌표설정까지 할 수 있다. Python 사용자들에게는 지도 기능과 관련된 만능 라이브러리라고 할 수 있다.
Folium으로 그려진 지도 객체는 HTML 파일로 저장할 수 있는데, 이를 통해 Frontend에서 화면으로 보여주기도 편리하다. 다만, 모바일 앱을 만드는 경우 웹 뷰를 보여주기 위한 웹 서버가 따로 필요해서 어플리케이션 쪽으로 응용하는 것은 조금 귀찮은 일이 된다고 한다. (나도 잘 모르지만 예전에 팀원분이 말해주셨다.)
다음은 최적화된 경로를 Folium 지도로 시각화하는 코드와 그림을 보여준다. 여기서 코드는 내가 Folium을 연습하면서 짰기 때문에, 단순히 기능을 확인하기 위한 필수적이지 않은 코드도 포함되어있다.
m = folium.Map(location = [cen_x, cen_y], zoom_start = 15)
# Marker = tooptip message before click + popup message after click + icon shape and color
# popup = simple strings, html, dataframe, graph
html1 = """
<h1>Seoul</h1><br>
<p>
Seoul, officially the Seoul City, is the capital and largest metropolis of South Korea.
</p>"""
df_test = pd.DataFrame(data = [[2000, 9879000],
[2010, 9796000],
[2020, 9963000]], columns = ['Year', 'Pop'])
html2 = df_test.to_html(classes = "table table-striped table-hover table-condensed table-responsive")
tooltip = 'Click Me!'
folium.Marker([cen_x + 0.001, cen_y + 0.001], popup = '<b>Seoul Station</b>', tooltip = tooltip,
icon = folium.Icon(color = 'red', icon = 'info-sign')).add_to(m)
folium.Marker([cen_x - 0.001, cen_y - 0.001], popup = html2, tooltip = tooltip,
icon = folium.Icon(color = 'green', icon = 'bookmark')).add_to(m)
folium.Marker([cen_x - 0.005, cen_y - 0.005], popup = html1, tooltip = tooltip,
icon = folium.Icon(color = 'blue', icon = 'flag')).add_to(m)
m.add_child(folium.ClickForMarker(popup = 'Marker added')) # Adding Marker on every click
# Circle
folium.CircleMarker([37.560704, 127.038819], popup = '<b>Wangsimni Station</b>', radius = 30, color = 'purple',
fill = True, fill_color = 'purple').add_to(m)
m.add_child(folium.LatLngPopup()) # Show Coordinates on every click
m.add_child(plugins.MiniMap()) # Minimap right below and manipulation
MousePosition().add_to(m) # continuously show mouth coordinates
#plugins.Terminator().add_to(m) # Day and Night
HeatMap(cities[:, 0:2], radius = 15).add_to(m)
AntPath(locations = cities[:, 0:2], reverse = 'True', dash_array = [20, 20]).add_to(m)
m.fit_bounds(m.get_bounds())
m.save("Map.html") # Save to HTML
m
Folium을 활용하여 예쁘게(?) 최적경로가 그려졌다.
Summary
이렇게 해서 D-Wave Quantum Annealing에 대한 기초지식 및 TSP와 연관된 간단한 수준의 예제 프로젝트를 경험하였다.
내 기준에서 양자컴퓨팅은 아직 많이 어렵다고 느낀다. 학부 4학년때 양자정보학 강의를 들었는데 초반에는 기초적인 양자역학 내용이어서 어느정도 따라갈 수 있었지만, 후반에 Bell State 개념이 나오고, 양자역학을 이용한 통신을 공부하면서 엄청나게 어려웠던 기억이 있다. 그때 배웠던 내용은 게이트 모델 기반의 양자컴퓨팅이었다.
반면 오늘 다룬 양자어닐링은 특정한 종류의 최적화 문제만을 제한적으로 잘 풀 수 있는 것 같다. 즉, 일종의 제한조건 양자컴퓨팅이며 보편적인 연산은 아니다. 그럼에도 최근 몇년동안 이와 연관된 물리연구가 종종 발표되고 있으므로, 기초정도는 알아둬야 할 것 같아서 공부하여 내용을 정리하였다. 나중에 시간이 되면 학부수준의 선형대수와 양자역학을 다시 복습하고 싶은데, 회사 다니면서 CS 지식 익히기도 시간이 부족하다.
요즘 양자컴퓨팅의 흐름은 Google이나 IBM에서 개발하는 게이트 기반 양자컴퓨팅이 보다 보편적인 트렌드 같다. 그래서 D-Wave 기술이 미래까지 살아남을 수 있는 기술인지에 대해서는 조금 회의적이다. 그러나 프로그래밍 사용자 관점에서 쓰기 편하게 되어 있고, 특히 그래프 관련 최적화 수단을 많이 제공하고 있으므로 경우에 따라서는 좋은 최적화 도구가 될 수 있을 것 같다.
References
- https://us-east-1.console.aws.amazon.com/braket/home?region=us-east-1#/landing : Example Codes in D-Wave Braket Jupyter notebook instances.
- https://docs.dwavesys.com/docs/latest/doc_getting_started.html : D-Wave Tutorial Pages
- https://en.wikipedia.org/wiki/Travelling_salesman_problem : TSP
- https://www.nature.com/articles/nature10012 : Quantum Annealing paper
- https://scikit-learn.org/stable/modules/clustering.html : Sklearn Clustering
- http://python-visualization.github.io/folium/ : Folium
'02. 물리학' 카테고리의 다른 글
| Introduction to VASP for DFT Simulation (0) | 2025.01.02 |
|---|